牛客多校,第三场。
若有公式图片无法正常显示,请使用梯子访问!
B - Classical String Problem
-
题意:
给定一个字符串,在执行n此操作,操作 ‘A’ 表示将前x位字符移动到字符串末尾,若x位正数则表示将末尾x位字符移动到字符串头部。操作 ‘M’ 表示查询第x位字符。 -
思路:
- 如果这个题使用substr()与字符串拼接会超时。
- 观察这个移动的操作,不难发现其实每次操作都是在单个字符串上进行。
- 可以构造出三倍长度的字符串,设定两个指针在一倍长度位置和二倍长度位置,例如x=2,即将两个指针都向右移两位,此时两指针中间的字符串即为操作后的字符串。
- 查询操作只需要根据指针的位置查询即可。还需要注意处理边界条件即可。
int main()
{
IOS;
string s;
cin >> s;
int l=s.size();
s+=s;
s+=s;
int n;
cin >> n;
int t1=l,t2=l-1;
while (n--)
{
char c;
int k;
cin >> c >> k;
if (c == 'M')
{
t1+=k,t2+=k;
if(t1<0)
{
t1+=l;
t2+=l;
}if(t2>l*3)
{
t1-=l,t2-=l;
}
}
else
cout << s[(t1+k-1)%l] << "\n";
}
return 0;
}
C - Operation Love
-
题意:
输入20个点的坐标,这些点可以在坐标系中描绘出一个手的形状。已知左手右手为镜像对称,判断输入的坐标描绘的是左手还是右手。 -
思路:
据说有个叉乘的向量做法。。但是似乎我写了一堆特判也卡过了呢(笑)
这个手中只有最下面的那条边是最长的,长度为10,左手与右手的区别就在于这条边的相邻两条边长度不一样。可以通过判断坐标位置和来判断最右手,特判见code。
double x[21], y[21];
double Len(int a, int b)//求两点间距离
{
return sqrt((x[a] - x[b]) * (x[a] - x[b]) + (y[a] - y[b]) * (y[a] - y[b]));
}
int main()
{
int T;
cin>>T;
while (T--)
{
for (int i = 1; i <= 20; i++)
cin>>x[i]>>y[i];
int maxa = 1, maxb = 20;
double maxlen = Len(maxa, maxb);
double lin;//最长边,=10
for (int i = 2; i <= 20; i++)
{
lin = Len(i, i - 1);
if (lin > maxlen)
{
maxlen = lin;//最长边
maxa = i;//最长边的对应两点
maxb = i - 1;
}
}
int sta = maxa + 1;//最长边的相邻两点
int stb = maxb - 1;
if (sta > 20)
sta = 1;
if (stb < 1)
stb = 20;
double lena = Len(sta, maxa);//最长边的相邻两条边
double lenb = Len(stb, maxb);
bool ans;
if (x[maxa] - x[maxb] == 0)//是否为横向
{
if (y[maxa] - y[maxb] > 0)//输入是否为逆时针
{
//手朝右向时 手朝左向时
if ((lena > lenb && x[sta] > x[maxa]) || (lena < lenb && x[sta] < x[maxa]))
ans = 0;
else
ans = 1;
}
else//顺时针时结论相反
{
if ((lena > lenb && x[sta] > x[maxa]) || (lena < lenb && x[sta] < x[maxa]))
ans = 1;
else
ans = 0;
}
}
else
{
if (y[maxa] - y[maxb] == 0)//手不为横向但为纵向时
{
if (x[maxa] - x[maxb] > 0)
{
if ((lena > lenb && y[sta] > y[maxa]) || (lena < lenb && y[sta] < y[maxa]))
ans = 1;
else
ans = 0;
}
else
{
if ((lena > lenb && y[sta] > y[maxa]) || (lena < lenb && y[sta] < y[maxa]))
ans = 0;
else
ans = 1;
}
}
else//手不为固定时
{
if (x[maxa] > x[maxb])
{
if ((lena > lenb && y[sta] > y[maxa]) || (lena < lenb && y[sta] < y[maxa]))
ans = 1;
else
ans = 0;
}
else
{
if ((lena > lenb && y[sta] > y[maxa]) || (lena < lenb && y[sta] < y[maxa]))
ans = 0;
else
ans = 1;
}
}
}
if (ans)
cout<<"right"<<"\n";
else
cout<<"left"<<"\n";
}
return 0;
}
E - Two Matchings
- 题意:
补这个题是真的难受,题意都给我看晕了。出题人老阅读理解了。
题意这样理解会比较好:
有一索引序列P,并存在 x, y 索引,Px=y,Py=x;
则有(两层套娃,多想下)
那么此时满足P是(x,y)索引的二元组。此时x,y索引在长度为2的数组a中的花费为:
那么问题为:此时有一个序列由以上若干个a序列构成,构造出两个代表最小花费和次小花费的P序列,P序列要求:- P 由 1, 2, 3… n 组成
求这两个P序列在a中所得的最小与次小花费之和。
- 思路:
- 最小值的情况: 假设a序列长度为4,且元素为{1,1,2,5},那么此时满足花费最小的P序列为{2,1,4,3}.那么易得只需要将输入的a序列排序后按照P={2,1,4,3}计算花费,即可得最小花费。
- 次小值的情况: 依然是a={1,1,2,5},那么此时观察P序列,我们还能使用的P序列只有两种情况: P={3,4,1,2}; P={4,3,2,1},这里以P={3,4,1,2}为例,画个图观察下P序列中次小值与最小值之间的关系:
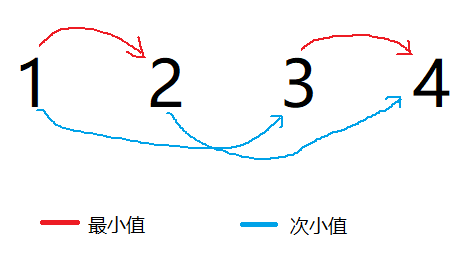
那么,由于a序列是一个排好序的序列, 如|a[3]-a[1]|=|a[3]-a[2]|+|a[2]-a[1]|,可得上图中的4个箭头可以转换为两条1->4的箭头,可得次小值为2*|a[4]-a[1]|。可以尝试下P={4,3,2,1}时,也是同样的结果。 - 当a序列的长度大于4时: 假设a序列长度为4时,同上推导依然是2*|a[6]-a[1]|; 当长度大于6时,则可以将这个P序列拆开来处理,因为4,6可以表示出所有偶数,例如8=4+4,10=4+6….
- 那么根据长度为4,6的两种情况,就可以列出了转移方程:
dp[i] = min(dp[i - 4] + v[i - 1] - v[i - 4], dp[i - 6] + v[i - 1] - v[i - 6]);
其中是截取上一步长度为4或6的情况来转移,根据当前位置的前4位或者前6位的最小值来进行转移。
我发誓这是我博客里面写的最长的一个单题题解!!!累死了
ll dp[200005];// long long
int main()
{
IOS;
int T;
cin >> T;
for (int ts = 0; ts < T; ++ts)
{
int n;
cin >> n;
vector<ll> v;
for (int i = 0; i < n; ++i)
{
ll tmp;
cin >> tmp;
v.push_back(tmp);
}
sort(v.begin(), v.end());
dp[0] = 0;
dp[4] = v[3] - v[0];
dp[6] = v[5] - v[0];
dp[8] = v[7] - v[4] + dp[4];
for (int i = 10; i <= n; i += 2)
dp[i] = min(dp[i - 4] + v[i - 1] - v[i - 4], dp[i - 6] + v[i - 1] - v[i - 6]);
cout << dp[n] * 2 << endl;//别忘了是两个箭头
}
return 0;
}
G - Operating on a Graph
-
题意:
给定一个 n 个点的图,第 i 个点一开始是第 i 种颜色,输入m条边,表示两种颜色(点)之间有一条边。接着有 q 次操作,第 i 次操作指定一个点 oi,表示第 oi 种颜色会侵略所有与自己相邻的颜色,求最终每个点的颜色。 -
思路:
图论+并查集
- 这个题并不仅仅是将oi颜色的邻居变为oi的颜色,难点在于将自己邻居的颜色所对应的所有点变为oi颜色。
- 首先开一个链表组G(类似与邻接表存图),储存两种颜色的边(这里应理解为颜色)。
- 在每一次oi操作时,将oi相邻颜色gcol的集合的颜色变为oi,并将gol的集合合并到oi上,这样在下一次还是处理oi时就能直接访问到所有oi颜色的邻居(类似预处理)。
const int N = 8e5 + 5;
int s[N];
// 初始化函数
list<int> G[N];
void init(int n)
{
for (int i = 0; i < n; i++)//颜色编号从0开始
{
G[i].clear();
s[i] = i;
}
}
int find(int x)//并查集
{
if (x != s[x])
s[x] = find(s[x]);
return s[x];
}
int main()
{
IOS;
int T;
cin>>T;
while(T--)
{
int x,y;
int n,m;
cin>>n>>m;
init(n);
for(int i=0;i<m;i++)
{
cin>>x>>y;
//类似于存图,不过这里应理解为 x与y‘颜色’为邻居,而不是x与y点为邻居。
G[x].push_back(y);
G[y].push_back(x);
}
int q,o;
cin>>q;
while(q--)
{
cin>>o;//要处理的oi颜色
if(find(o)!=o)
continue;//若oi颜色不存在,不处理
list<int>res;
for(auto ot:G[o])//所有oi颜色的邻居
{
int gcol=find(ot);
if(gcol!=o)//如果邻居节点的颜色还不为oi,就需要处理
{
s[gcol]=o;
//将oi颜色的邻居的邻居存入,便于下一次处理
res.splice(res.end(),G[gcol]);
}
}
swap(res,G[o]);
}
for(int i=0;i<n;i++)
cout<<find(i)<<" ";
cout<<endl;
}
return 0;
}